2022年单招考试数学复习题
一、选择题:(每题5分,共28道,共计140分)
1.方程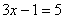 的解为( )
的解为( )
A.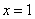 B.
B. 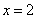 C.
C.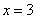 D.
D.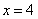

2.若 ,则
,则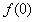 的值为( )
的值为( )
A.0 B.1 C.-2 D.-3
3.用列举法表示集合: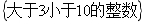 ,正确的是( )
,正确的是( )
A.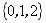 B.
B.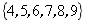 C.
C.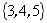 D.
D.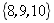
4.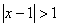 的解集为( )
的解集为( )
A.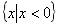 B.
B.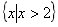 C.
C.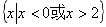 D.
D.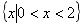
5.函数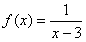 的定义域为( )
的定义域为( )
A. 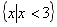 B.
B. 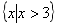 C.
C. 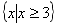 D.
D.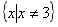
6.函数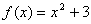 的值域是( )
的值域是( )
A.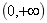 B.
B. 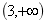 C.
C. 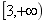 D.
D. 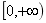
7.已知函数 在R上为偶函数,则
在R上为偶函数,则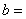 ( )
( )
A.0 B.1 C.2 D.-1
8.在指数函数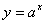 中,
中, 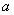 的取值范围是( )
的取值范围是( )
A.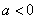 B.
B.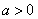 C.
C.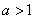 D.
D.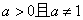
9.偶函数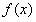 在
在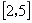 上为减函数,最小值为7,则
上为减函数,最小值为7,则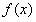 在
在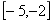 上是( )
上是( )
A.增函数且最小值为7 B. 增函数且最大值为7
B. 减函数且最小值为7 D. 减函数且最大值为7
10.若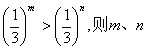 的大小关系是( )
的大小关系是( )
A.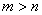 B.
B.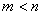 C.
C. D.无法确定
D.无法确定
11.已知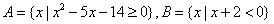 ,则
,则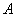 是
是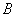 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.命题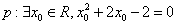 ,则命题
,则命题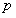 的否定是( )
的否定是( )
A. 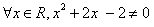 B.
B. 
C. 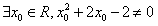 D.
D. 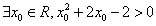
13.若方程x2-2mx+4=0的两根满足一根大于1,一根小于1,则m的取值范围是( )
A.(-∞,-2) B.(-∞,-2)∪(2,+∞) C.(2,+∞) D.(-2,+∞)
14.下列函数中,在区间(1,2)内有零点的函数是( )
A.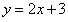 B.
B.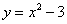 C.
C.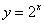 D.
D.
15.sin14ºcos16º+cos14ºsin16º的值是( )
A. B.
B.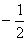 C.
C.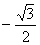 D.
D.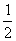
16.已知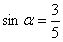 ,且角的终边在第二象限,则
,且角的终边在第二象限,则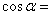 ( )
( )
A.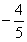 B.
B.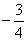 C.
C. 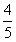 D.
D. 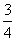
17.在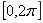 上满足
上满足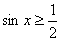 的
的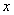 的取值范围是( )
的取值范围是( )
A.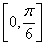 B.
B.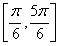 C.
C.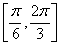 D.
D.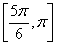
18.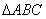 中,若
中,若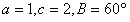 ,则
,则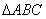 的面积为( )
的面积为( )
A.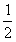 B.1 C.
B.1 C.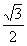 D.
D.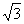
19.若→·→+→2=0,则△ABC必定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
20.已知向量 ,则
,则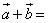 ( )
( )
A.-1 B.3 C.(2,1) D.(3,0)
21.已知平面向量 ,则
,则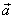 与
与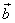 的夹角是( )
的夹角是( )
A.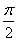 B.
B.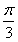 C.
C. D.
D.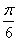
22.在等差数列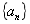 中,
中,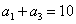 ,则
,则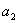 的值为( )
的值为( )
A.5 B.6 C.8 D.10
23.已知复数z满足(1-i)z=2+i,则z的共轭复数在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
24.已知直线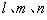 及平面
及平面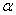 ,下列命题中的假命题是( )
,下列命题中的假命题是( )
A.若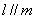 ,
,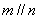 ,则
,则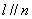 .
.
B.若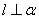 ,
,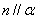 ,则
,则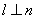 .
.
C.若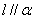 ,
,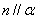 ,则
,则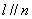 .
.
D.若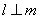 ,
,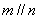 ,则
,则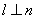 .
.
25.直线x+y-2=0与圆x2+y2=4相交于A,B两点,则弦AB的长度等于( )
A.2 B.2 C. D.1
26.已知圆柱的底面直径与高 都等于球的直径,则圆柱的
都等于球的直径,则圆柱的 体积与球体积之比为( )
体积与球体积之比为( )
A.1∶2 B.2∶1 C.2∶3 D.3∶2
27.同时掷两个骰子,其中向上的点数之和是5的概率( )
A.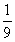 B.
B.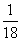 C.
C.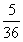 D.
D.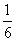
28.容量为20的样本数据,分组后的频数如下表:则样本数据落在区间[10,40)的频率为( )
分组 |
[10,20) |
[20,30) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
频数 |
2 |
3 |
4 |
5 |
4 |
2 |
A.0.35 B.0.45 C.0.55 D.0.65
二、填空题(每题5分,共20道,共计100分)
1.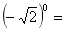 _______
_______
2.若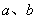 互为相反数,则
互为相反数,则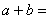 ________
________
3. 已知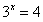 ,则
,则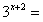 ______
______
4.设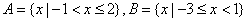 ,则
,则
5.已知函数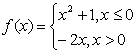 ,若
,若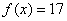 ,则
,则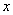 =
=
6.若直角坐标内的点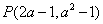 在第四象限,则
在第四象限,则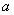 的取值范围为____________
的取值范围为____________
7.如果函数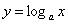 的图象过点(9,2),则
的图象过点(9,2),则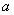 = ________
= ________
8.计算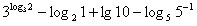 =
=
9.已知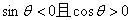 ,则角
,则角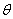 一定在第______象限
一定在第______象限
10.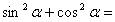
11.已知函数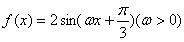 的最小正周期为
的最小正周期为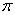 ,则
,则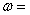 .
.
12.若直线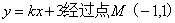 ,则k=______
,则k=______
13. 在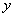 轴上的截距为2且倾斜角为45°的直线方程为
轴上的截距为2且倾斜角为45°的直线方程为
14.已知x,y为正实数,且满足4x+3y=12,则xy的最大值为________.
15.若直线l1:ax+2y=0和直线l2:2x+(a+1)y+1=0垂直,则实数a的值为________.
16. 等比数列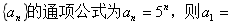
17.正方体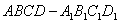 中,异面直线
中,异面直线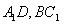 所成的角大小为
所成的角大小为
18.椭圆9+2=1的焦点为F1,F2,点P在椭圆上.若|PF1|=4,则|PF2|=________
19. 8名世界网球顶级选手在上海大师赛上分成两组,每组各4人,分别进行单循环赛,每组决出前两名,再由每组的第一名与另一组的第二名进行淘汰赛,获胜者角逐冠、亚军,败者角逐第3、4名,大师赛共有________场比赛.
20.某田径队有男运动员30人,女运动员10人.用分层抽样的方法从中抽出一个容量为20的样本,则抽出的男运动员有 人.
三、解答题:(每题10分,共6题,共计60分)
1.若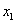 和
和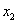 分别是一元二次方程
分别是一元二次方程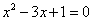 的两根,求
的两根,求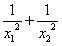 的值?
的值?
2.化简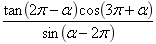
3.已知不等式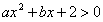 的解集为
的解集为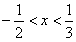 ,求
,求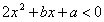 的解集?
的解集?
4.已知两条平行直线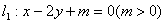 与
与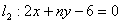 之间的距离是
之间的距离是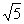 ,求m+n的值?
,求m+n的值?
5.已知二次函数f(x)的图像过点A(-1,0)、B(3,0)、C(1,-8).
(1)求f(x)的解析式;
(2)求f(x)在x∈[0,3]上的最值;
6.已知函数f(x)=2cos2x-sin xcos x-2sin2x.
(1)求f(x)的最小正周期;
(2)求f(x)的单调区间.